History of Calculation | History of calculating Devices (part-I)

History of calculating Devices

( Part-I )

2.1 Introduction to Calculating Devices:

 As we read, humans invented computers to do work easily; calculate and ease the burden of memory (remembrance). 

Just as there were many stages in the development of human beings moving towards civilization, in the same way there were many stages in the development of computers. 

Three thousand BC The history of Abacus to the present day microprocessor chip is the history of computers. 

In other words, we can also say that the history of instruments of calculation is the history of human progress. 

Stone Age man counted sheep by counting pieces of stone. The word 'calculate' in English is derived from the Latin word calculus, which means stone. Later humans learned to count with fingers. 

There are basically two methods of calculation:

• Counting (Digital Calculation ) 
• Calculating (Analog Calculation) 

To note that only man can do numerical calculation (like 25 x 3 = 75 etc. ). with the help of certified measures such as a meter, Centimeter, Kilograms, etc. 

in the calculation based on the given object is measured. As is obvious, there is absolutely no error in the numerical calculation while there is some mistake in the calculation. 

We can understand the difference between the two calculations from the example given. A needle in the car's speedometer shows the speed of the car by rotating on a scale facing the meter. This needle is attached to a wheel. With wheel car excel roams. 

In this way, the needle rotates according to the speed of the car. Measured by a standard speedometer in a scale mounted on a meter. 

Marks are made in By reading the same number of points on a scale made in this way, we tell the speed of the car. This is an example of an analog. 

On the other hand, there's the Car Odometer, which measures how many axles the car made. Since this meter measures the car's rounds, it can be called a mechanical or a mechanical device.

2.2 Sand Computers:

2500 years ago, Egyptian merchants built a computer using sand, pebbles and ballast. For this, he found a method by which calculation could be done without writing any number. 

In this method, three grooves of sand were made, of which the leftmost slot represented the unit and the leftmost slot represented the hundreds. 

When there were ten pebbles in the unit grooves, one of them was put into the middle groove. Similarly, when there were ten pebbles in the middle groove, a cucumber was inserted in the leftmost groove which displayed a hundred. In this way, this method was similar to the place value of modern mathematics.

2.3 Other Methods of Calculation:

 The people of Mesopotamia counted in units of sixty-sixty. Such a method is called the Hague Decimal method. In this, the digits were repeated again and again. 

For example, when they had to write 165, they would write 60 twice, four times 10 and five times 1, the same was calculated in many other ways. 

The people of Egypt had developed a type of decimal method. The digits 1 to 9 were repeated repeatedly to write a number. 

For 10 and its multiplier numbers, different signs were written 6 times and 1 mark 3 times. In the time of Confucius (2600 years ago), the Chinese knew the use of decimal but they did not know zero. 

Their method was based on Multiplication. He used to write numbers of 100 and 5 to write 500. The inhabitants of Rome used to write the numbers 100 and 5 to write 500. 

Frameworks were invented only later in China. Long before the Europeans, the Chinese had also assumed the value of 'pie' ('= 3.14). Indian mathematics started in the Vedic period itself. 

The texts called ‘Shulvasutra’ describe the method of making altars. Reading these formulas, it seems that their author was already aware of the principles of multiplication of Theorems and Squares from Pythagoras. 

Mathematicians of India could calculate the square root value of 2 exactly up to 12 places.

Centuries before the Gupta period, the two branches of Indian mathematics were Patti (arithmetic) and Algebra. 

Decimal method of digits, their local value (place value) and 'zero' were given by Indians. Later computers were made on zero information and decimal method. The world's first computer was based on the 'ENIAC' decimal system.

2.4 Abacus:

The word Abacus is derived from the Arabic word 'Abac', which means the flat surface of the sand. 

In this, sand used to spread from one end to the other in a wooden plank. In this sand, pebbles were made by making grooves. Later, the changed form of this frame was seen as Abacus. 

It used wood in place of sand and beads in place of pebbles. The wooden frame was first developed in China, from where it spread to Egypt, Greece, and Rome, etc. This simple device is still practiced in many modern countries like Russia, Japan, India, etc. to teach children counting. 

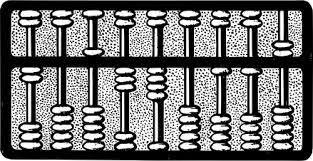figure 2.2 Chinese Abacus

Figure 2.3 (a) shows a Chinese abacus. It is a rectangular wooden frame with a mid-bar dividing from the middle. One part divided is smaller, called Heaven and the other part is larger, it is called Earth. 

Some wires have been placed crossing the mid-bar, which display unit, tens, hundreds, etc. from top to bottom. In each wire, 5 beads are threaded, each of which has a value of 1. Heaven has 2 pearls, each of which has a value of 5. 

In the abacus shown by the picture, there are 2 pearls in the earth and 1 pearl in heaven in the row of thousand, so the total value is 2 + 5 = 7. 

Similarly, in the lines of ten thousand, lakh, ten lakh, crore and ten crore respectively, (3 + 0 = 3), (4 + 0 = 4), (0 + 0 = 0), (1 + 5 = 6) respectively. , And (4 + 5 = 9) is displayed.

figure 2.3 (a) Chinese Abacus

Thus to add other numbers to the number displayed on the abacus, move the beads towards the mid-bar and in the opposite direction from the mid-bar to subtract. 

Abacus proved very useful for adding and subtracting simple digits, but it was not possible to do other calculations on multiplication, etc. 

2.5 Counting Board: 

At the beginning of the Middle Ages, the Calculus board was developed in the form of Abacus. These enamels were made from precious metals and were used in cafes, casinos, etc. of rich people. 

In those days, rich people used to come to the counters and pay the accounts. That's why the word counter came into vogue these days.

2.6 Analog Calculator:

In the Seventeenth Century, great revolutionary, social and scientific changes took place in Europe. With the development of science and technology, the need for faster computing machines began to be realized. 

The great mathematician of Scotland John Napier (1552-1617) invented Napier Bones and the logarithm at this time. At this time the slide rule was also invented.

2.7 Napier Bones:

 John Napier invented this method of calculation by digging up numbers on rectangular rods of ivory (first bones) to multiply and simplify parts. 

It consisted of ten rods, each of which was used for each digit of a decimal. There was also an eleventh rod, in which numbers were written for multiplication from 1 to 9.

Napier was the first man who uses the decimal point. The sticks are adjacent to each other to multiply. With these rods, the rods were placed on which multiplication points from 1 to 9 were written. 

Now if multiplying by 6, two hypothetical lines were drawn on the left in the fourth row with a 6k mark. Multiplication was taken by adding numbers written between these lines as shown in the picture. See Figure 2.4.

Fig-2.4: Multiplication by Napier Bones (485×6)

2.8 Logarithm:

 Jobst Bingie of Switzerland first discovered the logarithm, but the search for the logarithm was first published by John Napier, so his name was associated with the search. 

In this method, the logarithms of the given digits are multiplied by the table. These logarithms are added together and then viewed from the Antilogarithm table. 

Similarly, to calculate the power or square root, the logarithm of a given number and the power is multiplied. 

2.9 Slide Rule:

The German scientist William Oughtred invented the slide rule, which remained the main counting machine for three centuries. Inside the slide rule is a rule, between which the slide can be moved. 

Above them is a Cursor, with a line drawn between them. To multiply on the slide and the rule; there are two 'A' scales that are marked on the basis of logarithms. the product of 2 to 2 is shown inside the cursor. 

The method is explained. At point 2 of the lower 'A' scale, point 1 of the upper 'A' scale has been set by moving the slide and the cursor's baseline has been brought up to point 2 of the upper 'A' scale.

Slide Rule

The product of these two can be seen as 4 on the 'A' scale below. When the numbers are being multiplied in the slide rule, the corresponding distances are actually added on two logarithmic scales. 

In addition to multiplication, you can also calculate the square root, logarithm, radial calculations, inverse, the square inverse, the power of the three, the inverse of the three, etc. by the slide rule. 

Until about 1970, the slide rule was a common tool used by all engineers and scientists. After this, calculators with microprocessors became out of date as they became prevalent.

2.10 Pascal's calculator:

 In the seventeenth century, French mathematician and physicist Blaise Pascal (Fig. 2.6) created the automatic calculator. 

He named this model made of cycles and wheels, 'Pascaline'. This instrument, which was equal to about six persons, could not become popular due to expensive and then after the creation of this device, the rumor was also spread that due to this the public would become unemployed. 

fig. 2.6 Pascaline

However, this calculator of Pascal gave the automatic name 'Pascal'. Ten-tooth ratchet gear was used in this device (Fig. 2.7). 

After the completion of a cycle of ten teeth of the first unit cycle, one tooth of the ten cycle moved forward. These chakras were run with the help of hand-rotating wheels. The speed of the cycle was measured in dials (like the odometer of a car).

we will discuss Leibnitz's calculator, Punched Card, other mechanical calculators, Charles Babbage's Differential Engine, Analytical Engine, Lady Ada Lovelace, George Boole & Boolean Algebra, Hollerith's Punched Card Machine, electric calculators of the first half of the twentieth century. , Harvard Mark-1, German Computers & Development of Analog Computers in the next part. 

Click here for Next Part-II

Thanks for your valuable time...